Türev (derivative) Nedir?

Sayfa İçeriği

Tanımı

Türev Türkçe sözlükte değişken artması sıfıra giderken, işlev (function) artmasının değişken artmasına oranının sınırı (limit) olarak tanımlanmıştır. Sınır için “lim” kısaltması kullanılır.

Bu tanım aslında Teğet ve Kesen Nedir? konusununda verilen denklemin sözlü anlatımıdır. Ancak bu konuda yalnızca bir noktadan bahsedilmiştir. Şimdiki soru farklı bir nokta seçildiğinde ne olacağıdır. Doğrunun eğimi Eğim Nedir? konusunda da anlatıldığı üzere tüm noktalarda eşittir ancak bu durum eğriler için geçerli değildir. Eğrinin her noktası farklı bir eğime sahip olabilir. Bu durumda her noktada farklı bir teğet doğrusundan (tangent line) bahsedilir. Söz konusu olan işlev bir değişkenli değil de iki değişkenli olduğunda adı teğet düzlemi (tangent plane) olur. Çünkü bir noktadan artık tek bir doğru değil birden çok doğru geçmektedir ve bu doğrular bir düzlem oluştururlar. Şekil 1'de tek değişkenli bir işlev için iki farklı teğet doğrusu örneği verilmiştir. Verilen örnekte A ve B noktaları birbirlerine çok yakın olmalarına rağmen eğimleri ve doğal olarak teğet doğruları farklıdır.

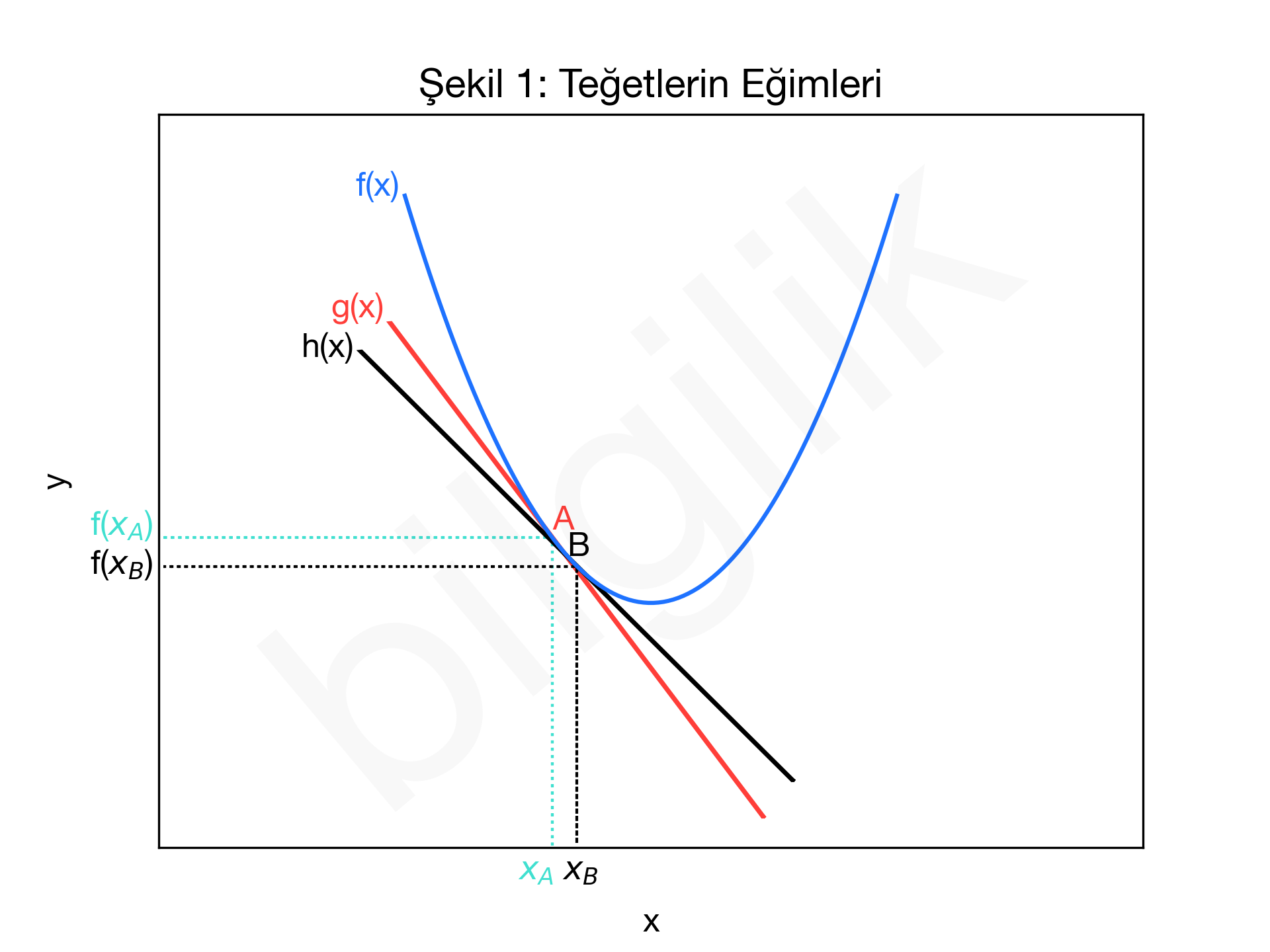
Bir eğri üzerindeki herhangi bir noktanın sınırı varsa o noktanın eğimi hesaplanabilir. Şekil 1'de verilen A ve B noktalarının eğimleri aşağıdaki şekilde hesaplanır:

$m_{A} = \lim_{u ⇾ 0} \frac{f (x_{A} + u) - f (x_{A})}{u}, m_{B} = \lim_{u ⇾ 0} \frac{f (x_{B} + u) - f (x_{B})}{u}$

Burada, x_A ve x_B sırasıyla A ve B noktalarının x koordinatları, u ise bu koordinatlara olan uzaklıktır. Yukarıda iki nokta için verilen denklemler noktalardan bağımsız hale getirildiğinde f(x) işlevi için aşağıda verilen denklem elde edilir:

$m = \lim_{u ⇾ 0} \frac{f (x + u) - f (x)}{u} = f' (x)$

f(x) işlevinin sınırı olan tüm noktalarında geçerli olan bu eğim denklemi “f(x) işlevinin türevi” olarak adlandırılır ve f′(x) şeklinde gösterilir. Türevin diğer bir gösterimi de ^d⁄_dxf(x) şeklindedir ve “f(x) işlevinin x'e göre türevi” olarak okunur. Burada dikkatlerden kaçmaması gereken nokta işlevin türevinin de işlevin kendisi gibi x değişkenine bağlı bir işlev olmasıdır.

Türev 0'a yaklaşan uzaklık nedeniyle “anlık değişim oranı” (instantaneous rate of change) olarak da adlandırılır. Sınır söz konusu olmadığında adı “ortalama değişim oranı” (average rate of change) olur.

Örnekler

Örnek 1: f(x)=a işlevinin x'e göre türevi nedir?

$f (x) = a \Rightarrow f (x + u) = a$

$\frac{d}{dx} f (x) = \lim_{u ⇾ 0} \frac{a - a}{u} = 0$

Örnek 2: f(x)=ax+b işlevinin x'e göre türevi nedir?

$f (x) = a x + b \Rightarrow f (x + u) = a (x + u) + b$

$\frac{d}{dx} f (x) = \lim_{u ⇾ 0} \frac{a (x + u) + b - (a x + b)}{u}$

$\frac{d}{dx} f (x) = \lim_{u ⇾ 0} \frac{a x + a u + b - a x - b}{u}$

$\frac{d}{dx} f (x) = \lim_{u ⇾ 0} \frac{a u}{u} = a$

Örnek 3: f(x)=ax²+bx+c işlevinin x'e göre türevi nedir?

$f (x) = a x^{2} + b x + c \Rightarrow f (x + u) = a {(x + u)}^{2} + b (x + u) + c$

$\frac{d}{dx} f (x) = \lim_{u ⇾ 0} \frac{a {(x + u)}^{2} + b (x + u) + c - (a x^{2} + b x + c)}{u}$

$\frac{d}{dx} f (x) = \lim_{u ⇾ 0} \frac{a (x^{2} + 2 x u + u^{2}) + b (x + u) + c - (a x^{2} + b x + c)}{u}$

$\frac{d}{dx} f (x) = \lim_{u ⇾ 0} \frac{a x^{2} + 2 a x u + a u^{2} + b x + b u + c - a x^{2} - b x - c}{u}$

$\frac{d}{dx} f (x) = \lim_{u ⇾ 0} \frac{2 a x u + a u^{2} + b u}{u}$

$\frac{d}{dx} f (x) = \lim_{u ⇾ 0} \frac{u (2 a x + a u + b)}{u}$

$\frac{d}{dx} f (x) = \lim_{u ⇾ 0} (2 a x + a u + b)$

$\frac{d}{dx} f (x) = 2 a x + b$

Örnek 4: f(x)=ax³+bx²+cx+d işlevinin x'e göre türevi nedir?

$f (x) = a x^{3} + b x^{2} + c x + d \Rightarrow f (x + u) = a {(x + u)}^{3} + b {(x + u)}^{2} + c (x + u) + d$

$\frac{d}{dx} f (x) = \lim_{u ⇾ 0} \frac{a {(x + u)}^{3} + b {(x + u)}^{2} + c (x + u) + d - (a x^{3} + b x^{2} + c x + d)}{u}$

$\frac{d}{dx} f (x) = \lim_{u ⇾ 0} \frac{3 a x^{2} u + 3 a x u^{2} + 2 b x u + a u^{3} + b u^{2} + c u}{u}$

$\frac{d}{dx} f (x) = \lim_{u ⇾ 0} \frac{u (3 a x^{2}) + u (3 a x u) + u (2 b x) + u (a u^{2}) + u (b u) + u (c)}{u}$

$\frac{d}{dx} f (x) = \lim_{u ⇾ 0} (3 a x^{2} + 3 a x u + 2 b x + a u^{2} + b u + c)$

$\frac{d}{dx} f (x) = 3 a x^{2} + 2 b x + c$

Kaynakça

Türk Dil Kurumu Başkanlığı, “Türk Dil Kurumu Sözlükleri”, https://sozluk.gov.tr/, 2024.

R. A. Adams, C. Essex, “Calculus A Complete Course”, Pearson Canada Inc., 2018.