Yönlü Türev (directional derivative)

Tanımı

Yönlü türev, tikel türevin (partial derivative) eksenler dışındaki ara yönlere uygulanmasıdır. Bunun anlamı şudur: tikel türevde girdilerdeki değişim yalnızca bir eksende yapılmakta, diğer eksen değerleri sabit kalmaktadır. Dolayısı ile eğim doğrusu türevi alınan eksene paralel olmaktadır. Yönlü türevde ise değişim birden çok eksende aynı anda yapılmakta, dolayısı ile eğim doğrusunun yönü eksenler arası bölge olmaktadır.

Bir f(x,y) işlevinin x değişkenine göre tikel türevini hatırlayacak olursak:

Burada yaptığımız işlem herhangi bir A noktası için x değişkenini u kadar artırmak veya eksiltmek, y değişkenini ise sabit tutmaktır. Şimdi yapmak istediğimiz işlem ise hem x hem de y değişkenlerinin değerlerini aynı anda artırmaktır.

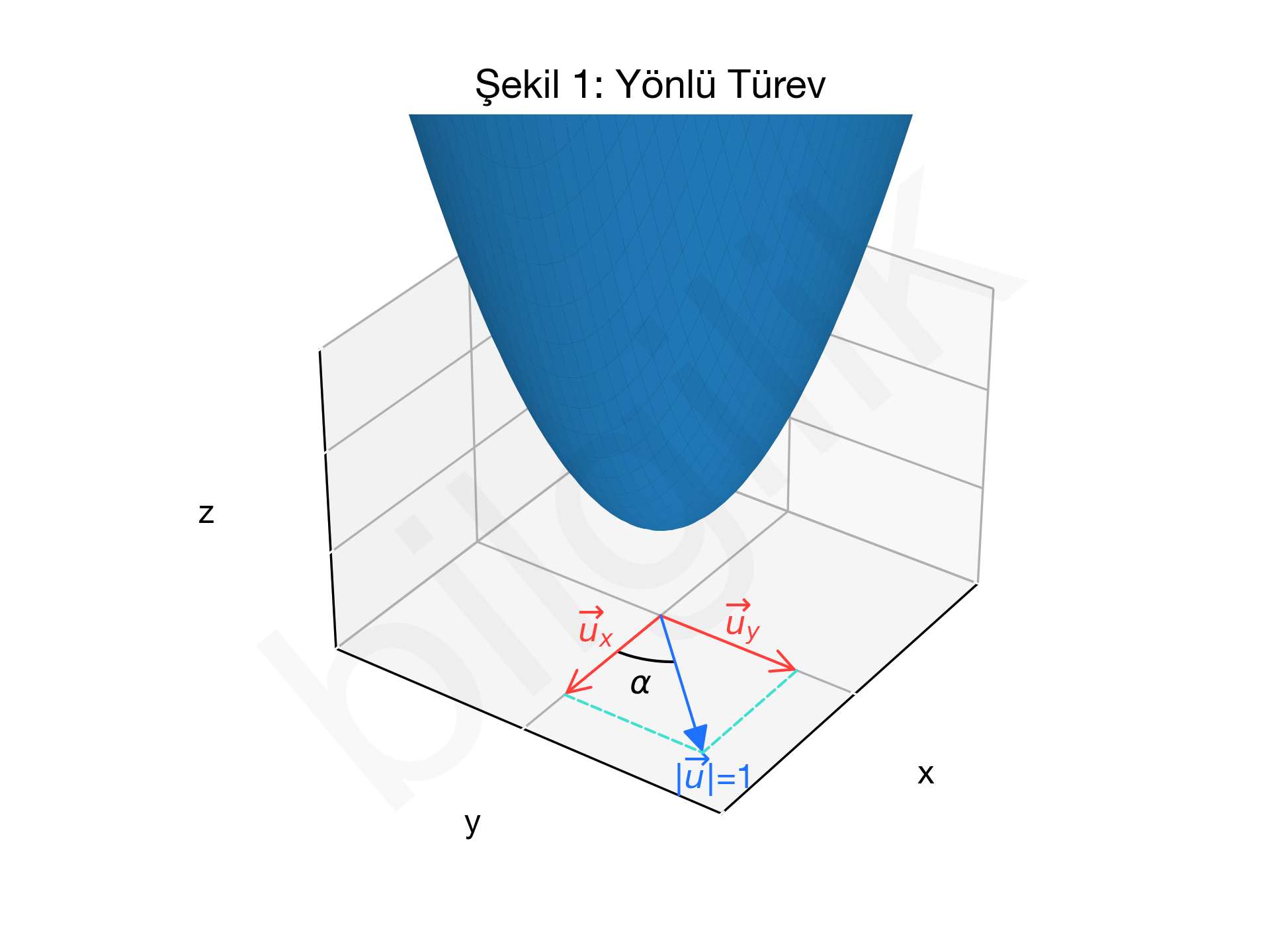
Şekil 1'de gösterilen u yöneyi üç boyutlu uzayda bizim değişim miktarını bulmak istediğimiz iki boyutlu (z=0) yön olsun. Bu yöney tikel türev sınır (limit) denkleminde kullanılan uzaklık (u) değişkenidir. Tikel türevde yönü eksenlerden birine paralel iken yönlü türevde yönü eksenler arası bir bölgedir. Bu tür ara yönlü değişimlerin gösterimi için temel yöneyler kullanılır. u yöneyinin temel yöneyler ile gösterimi aşağıda verilmiştir:

$$u=u_{x}i+u_{y}j=u\mathrm{cos(\alpha )}i+u\mathrm{sin(\alpha )}j$$

Burada α açısı u yöneyinin xy düzleminde (plane) x ekseni ile yaptığı açıdır. Dolayısı ile u yöneyinin x eksenindeki değişim miktarı u×cos(α), y eksenindeki değişim miktarı ise u×sin(α) kadardır. Bu durumda $D_{\overrightarrow{u}}f(x,y)$ ile gösterilen f(x,y) işlevinin u yöneyine göre yönlü türevi aşağıda verilen denklem olur:

$$D_{\overrightarrow{u}}f(x,y)=\underset{u⇾0}{\lim }\frac{f(x+u_x,y+u_y)-f(x,y)}{u}=\underset{u⇾0}{\lim }\frac{f(x+u\mathrm{cos(\alpha )},y+u\mathrm{sin(\alpha )})-f(x,y)}{u}\left(1\right)$$

Yukarıda verilen sınır hesabını kolaylaştırmak için tikel türevler kullanılabilir. Bunun için önce yukarıda verilen sınır denklemine benzer tek değişkenli bir işlev tanımlanır:

$$g(z)=f(x_0+z\mathrm{cos(\alpha )},y_0+z\mathrm{sin(\alpha )})\left(2\right)$$

Tanımlanan bu yeni işlevde tek değişken z'dir. Yeni işlevin z değişkenine göre türevi:

$$\frac{d}{\mathrm{dz}}g(z)=\underset{u⇾0}{\lim }\frac{g(z+u)-g(z)}{u}$$

Bu türevin z=0'daki değeri:

$$\frac{d}{\mathrm{dz}}g(0)=\underset{u⇾0}{\lim }\frac{g(u)-g(0)}{u}$$

Eşitlikteki g(u) ve g(0) yerine Denklem 2 konursa Denklem 1'e dönüşür:

$$\frac{d}{\mathrm{dz}}g(0)=\underset{u⇾0}{\lim }\frac{g(u)-g(0)}{u}=\underset{u⇾0}{\lim }\frac{f(x_0+u\mathrm{cos(\alpha )},y_0+u\mathrm{sin(\alpha )})-f(x_0,y_0)}{u}\Rightarrow \frac{d}{\mathrm{dz}}g(0)=D_{\overrightarrow{u}}f(x_0,y_0)\left(3\right)$$

x₀+zcos(α)=x ve y₀+zsin(α)=y kabul edersek Denklem 2 aşağıdaki şekle dönüşür:

$$x=x_0+z\mathrm{cos(\alpha )},y=y_0+z\mathrm{sin(\alpha )}\Rightarrow g(z)=f(x_0+z\mathrm{cos(\alpha )},y_0+z\mathrm{sin(\alpha )})=f(x,y)$$

g(z) işlevine çok değişkenli zincir kuralı uygulandığında:

$$\frac{d}{\mathrm{dz}}g(z)=\frac{d}{\mathrm{dx}}f(x,y)\cdot \frac{\mathrm{dx}}{\mathrm{dz}}+\frac{d}{\mathrm{dy}}f(x,y)\cdot \frac{\mathrm{dy}}{\mathrm{dz}}$$

$$\frac{d}{\mathrm{dz}}g(z)=\frac{d}{\mathrm{dx}}f(x,y)\cdot \mathrm{cos(\alpha )}+\frac{d}{\mathrm{dy}}f(x,y)\cdot \mathrm{sin(\alpha )}$$

Türevin z=0'daki değerine dönersek:

$$z=0\Rightarrow x=x_0+0\cdot \mathrm{cos(\alpha )},y=y_0+0\cdot \mathrm{sin(\alpha )}\Rightarrow x=x_0,y=y_0$$

$$\frac{d}{\mathrm{dz}}g(0)=\frac{d}{\mathrm{dx}}f(x_0,y_0)\cdot \mathrm{cos(\alpha )}+\frac{d}{\mathrm{dy}}f(x_0,y_0)\cdot \mathrm{sin(\alpha )}\left(4\right)$$

Denklem 3 ve 4'ü eşitlersek:

$$D_{\overrightarrow{u}}f(x_0,y_0)=\frac{d}{\mathrm{dz}}g(0)=\frac{d}{\mathrm{dx}}f(x_0,y_0)\cdot \mathrm{cos(\alpha )}+\frac{d}{\mathrm{dy}}f(x_0,y_0)\cdot \mathrm{sin(\alpha )}$$

x₀ ve y₀ değişken adları istenilen şekilde değiştirilebilir:

$$D_{\overrightarrow{u}}f(x,y)=\frac{d}{\mathrm{dx}}f(x,y)\cdot \mathrm{cos(\alpha )}+\frac{d}{\mathrm{dy}}f(x,y)\cdot \mathrm{sin(\alpha )}$$

Bu işlem boyut sayısından bağımsızdır. u×cos(α) ve u×sin(α) sırası ile u_x ve u_y yerine kullanıldığından asıl gösterime dönüldüğünde üç boyutlu örnek uzayda denklem aşağıdaki gibi olur:

$$D_{\overrightarrow{u}}f(x,y,z)=\frac{d}{\mathrm{dx}}f(x,y,z)\cdot u_x+\frac{d}{\mathrm{dy}}f(x,y,z)\cdot u_y+\frac{d}{\mathrm{dz}}f(x,y,z)\cdot u_z\left(5\right)$$

Özetle bir işlevin yönlü türevi, her bir eksen için bu eksene göre alınan tikel türev ile değişim miktarını bulmak istediğimiz yönü gösteren birim yöneyin bu eksendeki bileşeninin çarpımı sonrası tüm eksenlerden elde edilen sonuçların toplamıdır.

Denklem 5'te verilen eşitlik iki yöneyin nokta çarpımı olarak yazılabilir:

$$D_{\overrightarrow{u}}f(x,y,z)=\left(\begin{array}{c}\frac{d}{\mathrm{dx}}f(x,y,z)\\ \frac{d}{\mathrm{dy}}f(x,y,z)\\ \frac{d}{\mathrm{dz}}f(x,y,z)\end{array}\right)\cdot \left(\begin{array}{c}{u}_x\\ u_y\\ u_z\end{array}\right)\left(6\right)$$

Bu eşitlikte birinci yöney yöney türevin (gradient) bileşenleri, ikinci yöney ise eğim yönünü gösteren birim yöneyin bileşenleridir.

Neden Birim Yöney?

Denklem 6'da görüldüğü üzere eğim yönünü gösteren $\overrightarrow{u}$ yöneyinin büyüklüğü sonuç üzerinde etkilidir. Oysa istenilen şey bu yöneyin yalnızca yönü göstermesi, sonucu etkilememesidir.

$\overrightarrow{u}$ yöneyinin bir birim yöney olması:

• Yöneyin büyüklük (magnitude) etkisini ortadan kaldırarak yalnızca yönünün (direction) etkili olmasını sağlar.
• Farklı yönlerin kıyaslanmasında -ör. yöney türev (gradient)- tutarlılık (consistency) sağlar.

Kaynakça

R. A. Adams, C. Essex, “Calculus A Complete Course”, Pearson Canada Inc., 2018.

P. Dawkins, “Calculus”, tutorial.math.lamar.edu, 2022.